
Let we are get a book from a sofa and put it on the table. It is a very simple work. But we trying hard to move a loaded desk or a wall form one location to another. But it is not move a little. Here the technically second we cannot say it is a work. Because there are no displacements of the object (desk or wall) happened. Similarly, a coolie does not work when he or she standing with loaded bag. Although, he or she was feels tired. That is, if no displacement happens on the applied point of the force, then total work is zero.
Definition: “If we apply a force on a body and applied point of the force displaced then only work done.”
A force works in two ways
The amount of work done by a force is equal to the product of the force and the displacement of the point of application of the force in the direction of force.
Let, a force (P) applied on the point A of a body. After application of the force point A move to the point B. that is, total displacement of the applied point is AB = S
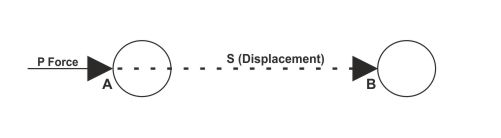
Therefore, total work (W)= applied force X displacement of the applied point of the force
That is, W = F X S
If displacement of applied point of force is not in the same direction of force
Let a force applied on a body (O) in the direction of B. That direction create an angle θ with the base OC. Therefore, the component of displacement is P cosθ
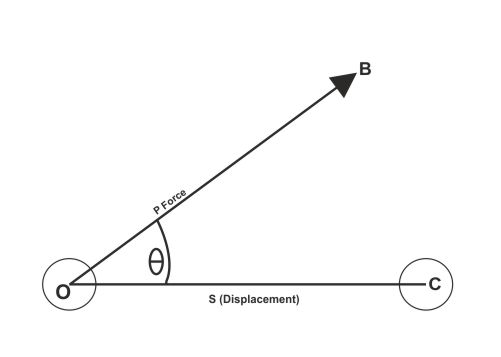
Therefore, The work (W)= P cosθ ✕ S
Work is a scalar quantity. Although force and displacement both are vector quantity but product of them is a scalar quantity.