The energy possessed by a body by virtue of its state of motion is called the kinetic energy.

Expression of kinetic energy

The kinetic energy possessed by a moving body is equal to the amount of work which the moving body performs before coming to rest. It can be calculated by applying an opposing force to stop the body and calculating the amount of work done by the opposing force.

Let, a body of mass m is moving with a velocity v. It is brought to rest by applying a constant opposing force F. Let, a, be the uniform retardation produced by the force and body travels a distance S before coming to rest. Then,

Retarding force F = m a

∴ Kinetic energy of the body = work done by the retarding force in stopping it.

∴ Kinetic energy K = Retarding force × displacement

∴ K = F × S

Now we calculate the displacement S, we have

Initial velocity (u) = v

Final velocity (v) = 0

Since a is the retardation, so acceleration = -a

∴ V² = u² +2 a S

∴ 0 = v² – 2 a S

∴ Displacement S = v² / 2a

∴ Kinetic energy K = ma (×) (v² / 2a) = ½ mv²

Work Energy theorem

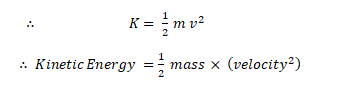
According the work-energy theorem, the work done by a force on a moving body is equal to the increase in its kinetic energy.

Let a body of mass m be moving with an initial velocity u. When a constant force F is applied on the body along its direction of motion, it produces acceleration a and the velocity of the body change from u to v in moving a distance S,

Force F = mass × acceleration = m . a

∴ W = F X S

Here, S = (v² – u²) / 2a

W = m a × ((v² – u²) / 2a)

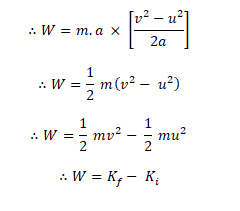
Thus we can say, work done on the body = Increase in kinetic energy